Question

A 80N force vector that makes an angle of 38° North of East (think Angle of Rotation!!!). Determine the horizontal and vertical components of the force.I need to do the following:1. Draw a free body diagram2. Identify Givens and Unknowns3. Identify the Equations4. Set up the equation using the givens and unknowns5. Solve

Answer 1

Horizontal : 49.25 N

Vertical :63.04 N

Step-by-step explanation

Step 1

Free body diagram

Step 2

Let

`\begin{gathered} V=\text{ 80 N}(\text{green)} \\ Vx=\text{unknown}(\text{red)} \\ V_y=unknow(\text{purple)} \\ \text{angle}=38(\text{yellow)} \end{gathered}`

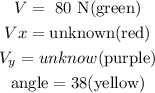
Step 3

equations and solution

as we have a rigth triangle, the x and y components of the vector are the sides of the triangle

hence

`\begin{gathered} V_y=V\cos 38(V_y\text{ is the adjacent side)} \\ \text{replace} \\ V_y=80N\cos 38 \\ V_y=63.04 \end{gathered}`

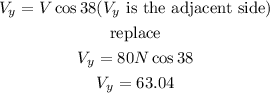
and

`\begin{gathered} V_x=Vsin38(V_x\text{ is the opposite side side)} \\ \text{replace} \\ V_x=80N\sin 38 \\ V_x=49.25 \end{gathered}`

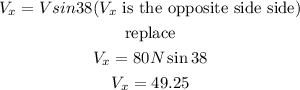
I hope this helps you