Question

Find the area a of the sector of a circle radius 50 centimeters formed by central angle1/10 radian

Answer 1

Given:

Radius of the circle = 50 cm

Central angle = 1/10 rad

Let's find the area of the sector.

To find the area of the sector, apply the formula:

`Area=(1)/(2)* r^2\theta`

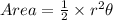
Where:

r is the radius = 50 cm

θ is the central angle in radians = 1/10 radian

Hence, we have:

`\begin{gathered} \text{Area}=(1)/(2)*50^2*(1)/(10) \\ \\ \text{Area}=(1)/(2)*2500*(1)/(10) \\ \end{gathered}`

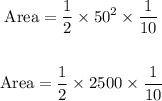
Solving further:

Therefore, the area of the sector of the circle is 125 square centimeters.

ANSWER:

125 cm²