Question

This is from my ACT prep guide workbookI am a beginner at this kind of math If you can, please explain step-by-step thoroughly on how to answer this problem :) thank you in advance

Answer 1

J. 63

Step-by-step explanation

We know that x is a positive integer and the other expression is also a positive integer. First, simplify the expression by taking x as a common factor,

`(x)/(3)+(x)/(7)+(x)/(9)=x((1)/(3)+(1)/(7)+(1)/(9))`

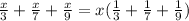
Then, add the coefficients. First, we have to find the least common denominator. 9 is a multiple of 3, and 7 is a primal number, thus the least common denominator is 9x7 = 63,

`x((1)/(3)+(1)/(7)+(1)/(9))=x(21+9+7)/(63)=x\cdot(37)/(63)`

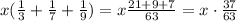
37 and 63 have no common factors, so that fraction cannot be simplified. As we can see there is a fraction multiplying x, but we were told that the expression was a positive integer, so we have to find x so that this expression results in an integer. Also, x must be an integer too. The least value of x is the one that cancels out the denominator of the fraction,

`x\cdot(37)/(63)=63\cdot(37)/(63)=37`

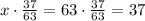
Hence, the least value of x is 63