Answer:
The resultant force on the object = 16.65 N
Step-by-step explanation:
The first force is 10N acting in in the direction N 45 degrees E
F₁ = 10N in the direction N 45 degrees E
The second force is 8N acting due South
F₂ = 8N due South
The diagram below illustrates the description
Resolve F₁ in the x and y direction
![\begin{gathered} F_(1x)=10\sin 45 \\ F_(1x)=\frac{10}{\sqrt[]{2}} \\ F_(1y)=10\cos 45 \\ F_(1y)=\frac{10}{\sqrt[]{2}} \\ F_1=F_(1x)i+F_(1y)j \\ F_1=\frac{10}{\sqrt[]{2}}i+\frac{10}{\sqrt[]{2}}j \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/q48xkqc7eftz9apydaiepjyd1imdi8w7u3.png)
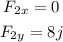
![\begin{gathered} R_x=\sum ^{}_{}F_x \\ R_x=F_1x+F_2x \\ R_x=\frac{10}{\sqrt[]{2}}+0 \\ R_x=\frac{10}{\sqrt[]{2}} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/hsimz1cxu125285blwm7c24lgqbacju2lj.png)
![\begin{gathered} R_y=\sum ^{}_{}F_y \\ R_y=F_(1y)+F_(2y) \\ R_y=\frac{10}{\sqrt[]{2}}+8 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/pfpefg0vth7qw5j3w9dt87o4usdwisbssr.png)
![\begin{gathered} R=R_xi+R_yj \\ R=\frac{10}{\sqrt[]{2}}i+(\frac{10}{\sqrt[]{2}}+8)j \\ |R|=\sqrt[]{(\frac{10}{\sqrt[]{2}})^2+(\frac{10}{\sqrt[]{2}}+8)^2} \\ R=\sqrt[]{50+227.14} \\ R=\sqrt[]{277.14} \\ R=16.65N \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/17kpjzztbrlcqs5x4mhn8ws56r0dqyhtpd.png)
The resultant force on the object = 16.65 N 1