Given:
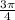
Required: Equivalent in degree
Solution:
Let the equivalent of
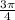
be represented as X.
Thus,
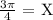
But
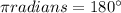
This implies that
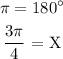
By cross-multiplication, we have
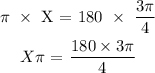
Divide both sides by the coefficient of X.
The coefficient of X is π.
Thus,
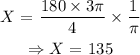
Hence, the equivalent of
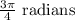
is 135°