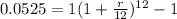Question

question 4 a savings and loan wants to offer a CD with a monthly compounding rate that has an APY of 5.25%. What annual nominal rate compounded monthly should it use ?

Answer 1

We are given a a savings and loan investment that offers a monthly compounding rate with an annual percentage yield (APY) of 5.25%.

We are now required to use this information to calculate the nominal rate of interest compounded monthly.

The compound interest formula for monthly compounding is given as;

`\begin{gathered} \text{Compound Interest (monthly):} \\ A=P(1+(r)/(n))^(tn) \end{gathered}`

Where the variables are;

`\begin{gathered} A=\text{Amount at the end of the investment period} \\ P=\text{Initial amount invested} \\ r=annual\text{ rate of interest} \\ n=\text{Number of times compounding is done per period} \\ t=\text{time, period of investment (in years)} \end{gathered}`

However, where we have the annual percentage yield already given, we can use that information to calculate the annual rate of interest as given by the formula below;

`\text{APY}=1(1+(r)/(n))^n-1`

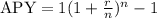
The variables given are;

`\begin{gathered} \text{APY}=5.25\%\text{ OR }0.0525 \\ n=12 \\ r=\text{?} \end{gathered}`

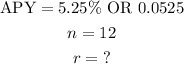
Substituting these into the formula we now have;

`0.0525=1(1+(r)/(12))^(12)-1`