Question

The point A(-2, 3) is translated using T: (x,y) (x+4, y+2).What is the distance from Ato A?

Answer 1

Ok, so

Here we have this linear transformation as follows:

`T\colon(x,y)=(x+4,y+2)`

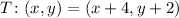
And we're going to translate the point A:

`A(-2,3)`

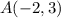
This is: (We replace the values of x and y of the point A in the transformation):

`\begin{gathered} T\colon(-2,3)=(-2+4,3+2) \\ T\colon(-2,3)=(2,5) \end{gathered}`

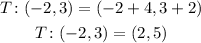
The point A translated will give us a new point B, which is (2 , 5) (After applying the transformation).

Now, let's find the distance between A (-2,3) and B (2,5).

Remember that the distance between two points:

`\begin{gathered} A(x_1,y_1) \\ B(x_(2,)y_2) \end{gathered}`

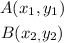
Can be found applying the following formula:

`D=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2}`

Replacing our values:

`\begin{gathered} D=\sqrt[]{(5-3)^2+(2-(-2))^2} \\ D=\sqrt[]{(2)^2+(2+2)^2} \\ D=\sqrt[]{4+16} \\ D=\sqrt[]{20} \end{gathered}`

Therefore, the distance between the points A and B, is √(20) units. (This is, approximately, 4.47)