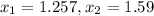We have the next equation
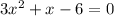
In order to solve this equation, we will use the next formula
![x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/li72dimqx1poek8bdg3bs589861h83kfxl.png)
where
a=3
b=1
c=-6
we substitute the values and reduce
![\begin{gathered} x_(1,2)=\frac{-1\pm\sqrt[]{1^2-4(3)(-6)}}{2(3)} \\ x_(1,2)=\frac{-1\pm\sqrt[]{73}}{6} \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/qvc2qzjkshlz4fb6oqfz4wwdu5rm2h0x2p.png)
if we have a second-degree equation we will have two solutions
first solution
![x_1=\frac{-1+\sqrt[]{73}}{6}=1.257](https://img.qammunity.org/2023/formulas/mathematics/college/6wq48q0s9v59f0uducpmpgfhq9gr4nf0wx.png)
the second solution is
![x_1=\frac{-1-\sqrt[]{73}}{6}=1.59](https://img.qammunity.org/2023/formulas/mathematics/college/5z95ur84irmpzuzwpd5vgnpciqbyxwr12v.png)
the two solutions of the equation are