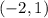Solution
- The function is positive where the values of f(x) are positive.
- But the interval which defines the portion for which the function is positive, are the x-values.
- Thus, we should just look at the parts of the table where f(x) is greater than 0 and write down the x-values corresponding to these f(x) values.
- Thus, we have that the interval over which the function is positive is:
![\begin{gathered} x\to f(x) \\ -2\to0 \\ -1\to2 \\ 0\to2 \\ 1\to0 \\ \\ \text{ Although }f(x)=0\text{ is not a positive value, we can include the x\_values corresponding} \\ \text{ to these f\lparen x\rparen values as long as we use open intervals.} \end{gathered}]()
Thus, the answer is