Step-by-step explanation:
We are given a sequence of numbers and each number as shown in the table labeled Sequence A is derived by multiplying the previous number by 2.
That is;
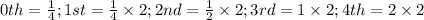
We can observe that the common ratio is 2, for every new term.
What we have is a geometric sequence and the variables are as follows;
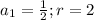
If we use the term number 1 as the first term (that is 1/2), then the formula for this sequence will be;

For the second term we observe that each next term is derived by adding 10 to the previous one. Hence we have;

The common difference here is 10, and we can see that sequence B is an arithmetic sequence. Using term 1 as the first term, and the common difference as 10, the nth term for this sequence will be;

To determine A(9), that is the 9th term for sequence A;

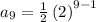
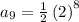
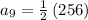
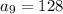
To determine B(9), that is the 9th term for sequence B;
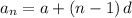
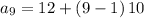
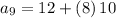
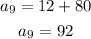
Therefore;
ANSWER:
