Given:
Slant height = 10 cm
Diameter = 12 cm
Let's find the surface area of the cone.
To find the surface area of the cone, apply the formula:

Where:
L is the slant height = 10 cm
r is the radius = diameter/2 = 12/2 = 6 cm
Plug in the values into the formula and solve for surface area A:
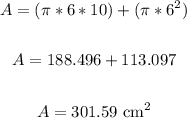
Therefore, the surface area of the cone to the nearest hundredth is 301.59 cm².
ANSWER:
301.59 cm²