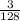General category: Sequences, Series, and Mathematical Induction
Sub-category: Formulas and Notation for Sequences and Series
Topic: Recursive Formulas and explicit Formulas.
Introduction:
Given a geometric sequence with the first term a_1 and the common ratio r, the nth term is given by the following formula:
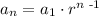
Step-by-step explanation:
If we have a geometric sequence whose common ratio is 1/2 and whose first term is 6, then the nth term is given by the following formula:
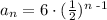
thus, if n= 9, we get:
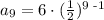
that is:
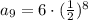
this is equivalent to:
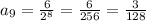
we can conclude that the correct answer is:
Answer:
The 9th term is: