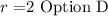Question

Which of the following polar functions does NOTproduce a conic section?

Answer 1

Let us begin by defining the equation of a conic section

The equation of a conic section usually takes the form:

For a conic with a focus at the origin, if the directrix is x =± p , where p is a positive real number, and the eccentricity is a positive real number e, the conic has a polar equation

`r\text{ = }\frac{ep}{1\text{ }\pm ecos\theta}`

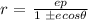
For a conic with a focus at the origin, if the directrix is y =± p , where p is a positive real number, and the eccentricity is a positive real number e, the conic has a polar equation

`r\text{ = }\frac{ep}{1\text{ }\pm\text{ esin}\theta}`

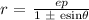
Looking through the options, we can see that the function that does not produce a conic section is:

`r\text{ =2 \lparen Option D\rparen}`