Question

A chemist mixes 500 milliliters of a solution that is 62% acid with 125 milliliters of a solution that is 27% acid. Do not do any rounding.

Answer 1

Hello there. To solve this question, we'll have to remember some properties about percentages.

Given that a chemist mixes 500 mililiters of a solution that is 62% acid with 125 mililiters of a solution that is 27% acid, we have to determine:

a) How many mililiters of acid are in the resulting mixture?

For this, we find how much is 62% of 500 and 27% of 125, adding the results.

62% of 500 can be calculated by multiplying:

`(62)/(100)\cdot500=62\cdot5=310\text{ ml}`

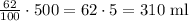
And 27% of 125 is calculated as:

`(27)/(100)\cdot125=(27)/(4)\cdot5=27\cdot1.25=33.75\text{ ml}`

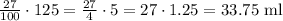
Adding the results, we have

`343.75\text{ ml}`

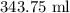
worth of acid in the mixture.

b) What percentage of the resulting mixture is acid?

For this, we find how many ml there are in the solution by adding:

`500+125=625`

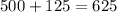
Now, we take the ratio between the amount of acid in the mixture we found in the last step and this number

`(343.75)/(625)=0.55`

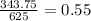
Multiplying by 100%, we get

`0.55\cdot100\%=55\%`

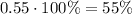
This is the result we were looking for.