Question

A library has a book sale to raise money. Hardcover books cost $4 each. Paperback books cost $2 each. Marvin goes to the sale and buys 12 total books. He spends $36. Write and solve a system of linear equations to find the numberof hardcover and paperback books he purchased.

Answer 1

This problem will lead us to a system of simultaneous equations.

Let x represent hardcover books,

Let y represent paperback books,

Therefore, we have:

`\begin{gathered} x+y=12\ldots(1) \\ 4x+2y=36\ldots(2) \end{gathered}`

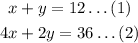
We will solve via the elimination method.

`\begin{gathered} \text{ We multiply eqn 1 by 2 and eqn 2 by 1 to get:} \\ 2x+2y=24\ldots(3) \\ 4x+2y=36\ldots(4) \\ \text{ Subtract eqn 3 from 4 to get:} \\ 2x=12 \\ \text{Divide both sides by 2 to get:} \\ x=(12)/(2)=6 \end{gathered}`

Having solved for x, we substitute this value of x into equation q to get y as:

`\begin{gathered} 6+y=12 \\ \text{ We subtract 6 from both sides to get:} \\ y=12-6=6 \end{gathered}`

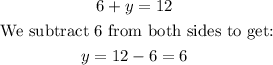
x = 6,

y = 6