Question

Find the vertex and the AOS for this problem y = 3x^2 - 6x + 5

Answer 1

In order to find the vertex of this quadratic equation, we can use the formula for the x-coordinate of the vertex:

`x_v=-(b)/(2a)`

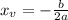
Where a and b are coefficients of the quadratic equation in the standard form:

`y=ax^2+bx+c`

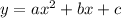
Using a = 3 and b = -6, we have:

`x_v=-(-6)/(6)=1`

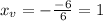
Now, to find the y-coordinate of the vertex, we just need to use the value of x_v in the equation:

`\begin{gathered} y=3\cdot1-6\cdot1+5 \\ y=3-6+5 \\ y=2 \end{gathered}`

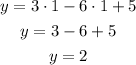
So the vertex coordinates are (1, 2).

The axis of symmetry (AOS) is the vertical line that passes through the vertex, so if the x-coordinate of the vertex is 1, the AOS will be x = 1.