Question

The probability that a customer will order a nonalcoholic beverage is .48b. Find the probability that in a sample of 12 customers, at least 5 will order a nonalcoholic beverage. (Round your answer to 4decimal places.)

Answer 1

Given:

probability of ordering non-alcoholic beverage = 0.48

probability of not ordering non-alcoholic beverage = 1 - 0.48 = 0.52

FInd: the probability that in a sample of 12 customers, at least 5 will order a nonalcoholic beverage.

Solution:

Recall the binomial probability formula.

`P(x)=nCr* p^r* q^(n-r)`

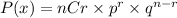
where

p = probability of success: 0.48

q = probability of failure: 0.52

n = the number of samples: 12

r = number of success (at least 5 which means not 1, 2, 3, or 4.

To determine the probability of having at least 5, let's calculate when r = 0, r = 1, r = 2, r = 3, and r = 4.

Let's start with r = 0 and solve.

`P(0)=_(12)C_0*0.48^0*0.52^(12)`
`\begin{gathered} P(0)=1*1*0.000390877 \\ P(0)=0.000390877 \end{gathered}`

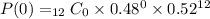
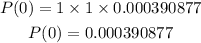
At r = 1,

`P(1)=_(12)C_1*0.48^1*0.52^(11)`
`\begin{gathered} P(1)=12*0.48^*0.000751686 \\ P(1)=0.0043297 \end{gathered}`

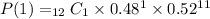
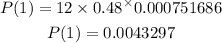
Now, let's solve for r = 2.

`P(2)=_(12)C_2*.48^2*.52^(10)`
`\begin{gathered} P(2)=66*.2304*.00144555 \\ P(2)=0.02198 \end{gathered}`

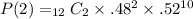
Moving on to r = 3.

`P(3)=_(12)C_3*0.48^3*0.52^9`
`\begin{gathered} P(3)=220*0.110592*0.0027799 \\ P(3)=0.067636 \end{gathered}`

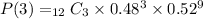
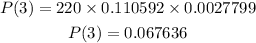
Then, lastly at r = 4.

`P(4)=_(12)C_4*0.48^4*0.52^8`
`\begin{gathered} P(4)=495*0.05308*0.00534597 \\ P(4)=0.14047 \end{gathered}`

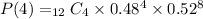
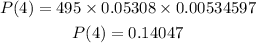
Let's now add the probability of getting r = 0, r = 1, r = 2, r =3, and r = 4 customers ordering a nonalcoholic beverage.

`P(0)+P(1)+P(2)+P(3)+P(4)`
`0.0043297+0.02198+0.067636+0.14047=0.2344157`
`0.000390877+0.0043297+0.02198+0.067636+0.14047=0.2348`

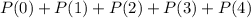
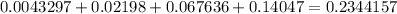
0.2348 is the probability of at most 4 customers ordering a non-alcoholic beverage.

Since the question is the probability of at least 5 customers ordering a non-alcoholic beverage which is the opposite of the at most 4 customers, then, let's subtract its probability from 1.

`1-0.2348=0.7652`

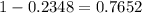
Therefore, the probability that in a sample of 12 customers, at least 5 will order a nonalcoholic beverage is approximately 0.7652.