Question

Just give best explanation and give answer to both questions

Answer 1

If the two triangles are similar then their angles have the same measure. This also implies that the quotient between a side of one triangle and its corresponding side in the other one is the same for the three pairs of sides. The sides of the large triangle are 9, 2+y and 12 and their corresponding sides in the small triangle are 3, 2 and x. Then since the quotient between corresponding sides is always the same we get:

`\begin{gathered} (9)/(3)=(2+y)/(2)=(12)/(x) \\ 3=(2+y)/(2)=(12)/(x) \end{gathered}`

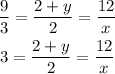
So for x we get:

`3=(12)/(x)`

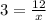
We multiply both sides by x and we get:

`\begin{gathered} 3\cdot x=(12)/(x)\cdot x \\ \\ 3x=12 \end{gathered}`

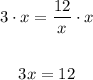
And we divide both sides by 3:

`\begin{gathered} (3x)/(3)=(12)/(3) \\ x=4 \end{gathered}`

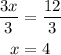
Then for y we get:

`3=(2+y)/(2)`

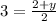
We can multiply both sides by 2:

`\begin{gathered} 3\cdot2=(2+y)/(2)\cdot2 \\ 6=2+y \end{gathered}`

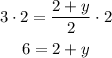
And we substract 2 from both sides:

`\begin{gathered} 6-2=2+y-2 \\ y=4 \end{gathered}`

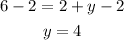
So x=4 and y=4. Then the answer to part 1 is option A and the answer to part 2 is option B.