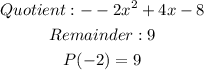Question

O POLYNOMIAL AND RATIONAL FUNCTIONSUsing the remainder theorem to evaluate a polync

Answer 1

Given;

There are given that the polynomial:

`P(x)=-2x^4-4x^3+4x^2-7`

Step-by-step explanation:

To find the quotient and remainder, we need to find the value of P(-2):

Then,

`\begin{gathered} P(x)=-2x^(4)-4x^(3)+4x^(2)-7 \\ P(-2)=-2(-2)^4-4(-2)^3+4(-2)^2-7 \\ P(-2)=-2(16)-4(-8)+4(4)-7 \\ P(-2)=-32+32+16-7 \end{gathered}`

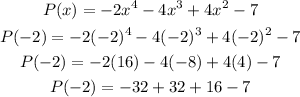
Then,

`\begin{gathered} P(-2)=-32+32+16-7 \\ P(-2)=16-7 \\ P(-2)=9 \end{gathered}`

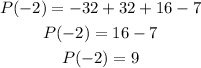
So, the remainder is 9.

Now,

For the quotient:

Divide the given polynomial by (x+2):

So,

`(-2x^4-4x^3+4x^2-7)/(x+2)=-2x^3+4x-8`

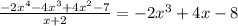
Final answer:

Hence, the quotient, remainder, and the value for P(-2) is shown below:

`\begin{gathered} Quotient:--2x^2+4x-8 \\ Remainder:9 \\ P(-2)=9 \end{gathered}`