In general, the simple interest formula is
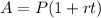
Where t is given in years.
And the interest is given by
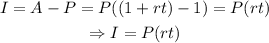
Let B the initial amount Lisa invested in the 10% interest account and C the amount she invested in the 8% account.
Therefore,
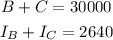
Expanding the second equation,
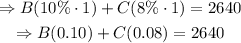
The system of equations becomes
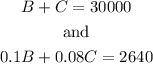
From the first equation, B=30000-C. Substitute into the second equation as shown below
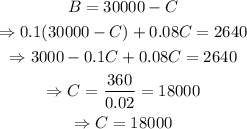
And
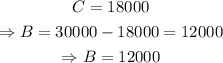
Therefore, she invested $12000 in the 10% account and $18000 in the 8% account.