The length of the rectangle is given to be x.
The width of a rectangle is 3 less than twice the length. This can be written mathematically to be:
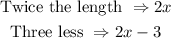
Therefore, we will have the rectangle to look as shown below:
The formula to calculate the perimeter of a rectangle is given to be:

Given that we have the following parameters:
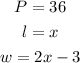
Substituting these values, we can get the value of x as shown below:
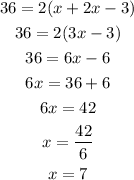
Given that the length has been calculated, we can get the width to be:

ANSWER
The length of the rectangle is 7 feet and the width of the rectangle is 11 feet.