Question

Triangle END is translated using the rule (x, y) → (x−4, y − 1) to create triangle E′N′D′. If a line segment is drawn from point E to point E′ and from point N to point N′, which statement would best describe the line segments drawn?

Answer 1

Given:

Triangle END is translated using the rule

`(x,y)\rightarrow(x-4,y-1)`

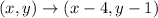
to create triangle E′N′D′.

Required:

We need to describe the line segment when a line segment is drawn from point E to point E′ and from point N to point N′,

Step-by-step explanation:

Let E(0,0), N(2,0), and D(0,2) be the points of the triangle END.

Use the translation rule to find the triangle E'N'D'.

Substitute x =0 and y =0 in the translation rule.

`E(0,0)\rightarrow E^(\prime)(0-4,0-1)`
`E(0,0)\rightarrow E^(\prime)(-4,-1)`

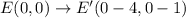
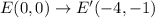
Substitute x =2 and y =0 in the translation rule.

`N(2,0)\rightarrow N^(\prime)(2-4,0-1)`
`N(2,0)\rightarrow N^(\prime)(-2,-1)`

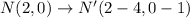
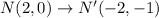
Substitute x =0 and y =2 in the translation rule.

`D(0,2)\rightarrow D^(\prime)(0-4,2-1)`
`D(0,2)\rightarrow D^(\prime)(-4,1)`

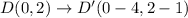
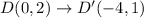
We get the point E'(-4,-1), N'(-2,-1), and D'(-4,1).

Mark the points E(0,0), N(2,0), D(0,2), E'(-4,-1), N'(-2,-1), and D'(-4,1) on the graph and draw a line segment from point E to point E′ and from point N to point N′,

From the figure, we get that the lines are parallel and congruent.

Final answer:

They are parallel and congruent.