Question

Find the measure of angles 1-7 that lines m and n are parallel and t is transversalm<1 =

Answer 1

First, from the diagram and the fact that lines m and n are parallel we get that:

1)

`39^(\circ)+\measuredangle1=180^(\circ).`

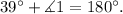
Therefore:

`\measuredangle1=180^(\circ)-39^(\circ)=141^(\circ).`

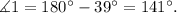
2) Angles 1 and 3 are opposed by the vertex, and the same occurs for angles 5 and 7, 4 and 6, and the angle of measure 39 degrees and 2, therefore:

`\begin{gathered} \measuredangle1=\measuredangle3\text{ }\Rightarrow\measuredangle3=141^(\circ), \\ \measuredangle2=39^(\circ), \\ \measuredangle5=\measuredangle7, \\ \measuredangle4=\measuredangle6. \end{gathered}`

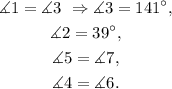
3) Angles 3 and 5 are alternate interior angles, and the same occurs for angles 2 and 4, therefore:

`\begin{gathered} \measuredangle5=\measuredangle3=141^(\circ), \\ \measuredangle4=\measuredangle2=39^(\circ). \end{gathered}`

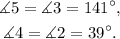
Answer:

`\begin{gathered} \measuredangle1=141^(\circ), \\ \measuredangle2=39^(\circ), \\ \measuredangle3=141^(\circ), \\ \measuredangle4=39^(\circ), \\ \measuredangle5=141^(\circ), \\ \measuredangle6=39^(\circ), \\ \measuredangle7=141^(\circ). \end{gathered}`