Question

I need to know the answer to the question please help me

Answer 1

The height of the triangle is 3 inches.

Explanation:

Given:

`\begin{gathered} \text{Base of the triangle}=3(2)/(5)\text{ inches} \\ \text{Area of the triangle}=5(1)/(10)\text{ inches} \end{gathered}`

We change the mixed fractions to improper fractions below:

`\begin{gathered} \text{Base of the triangle}=3(2)/(5)=((5*3)+2)/(5)=(17)/(5)\text{ inches} \\ \text{Area of the triangle}=5(1)/(10)=((10*5)+1)/(10)=(51)/(10)\text{ inches} \end{gathered}`

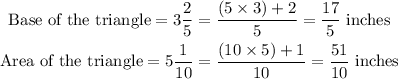
We want to find the height of the triangle.

Recall that the area of a triangle is calculated using the formula below.

`\text{Area}=(1)/(2)*\text{Base}* Height`

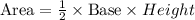
Substitute the given values:

`(51)/(10)=(1)/(2)*(17)/(5)*\text{Height}`

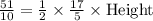
Multiply the numerators and denominators on the right side of the equation.

`\begin{gathered} (51)/(10)=(1*17)/(2*5)*\text{Height} \\ (51)/(10)=\frac{17*\text{Height}}{10} \end{gathered}`

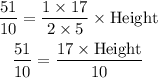
Multiply both sides by 10.

`\begin{gathered} (51)/(10)*10=\frac{17*\text{Height}}{10}*10 \\ \implies51=17*\text{Height} \end{gathered}`

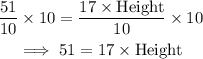
To solve for the height, divide both sides by 17.

`\begin{gathered} (51)/(17)=\frac{17*\text{Height}}{17} \\ 3=\text{Height} \\ \text{Height = 3 inches} \end{gathered}`

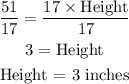
The height of the triangle is 3 inches.