Using the given pentagon, let's find the perimeter.
From the graph, we can deduce the vertices of the pentagon below:
(0, 9.5), (5.5, 7), (5.5, 0), (-5.5, 0), (-5.5, 7)
Let's find the perimeter.
To find the perimeter, let's first find the length of each side using the distance formula:
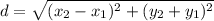
Now, let's label the figure:
Thus, we have the following:
• Length of AB:
Where:
(x1, y1) ==> (0, 9.5)
(x2, y2) ==> (5.5, 7)
We have:
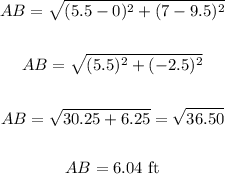
The length of AB = 6 ft
Also the length of AE will be 6 ft.
• Length of BC:
Where:
(x1, y1) ==> (5.5, 7)
(x2, y2) ==> (5.5, 0)
Thus, we have:
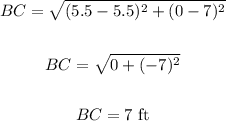
The length of BC = 7 ft
The length of DE will also be 7 ft.
• Length of CD:
Where:
(x1, y1) ==> (5.5, 0)
(x2, y2) ==> (-5.5, 0)
Thus, we have:
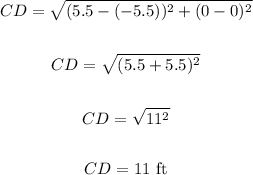
Therefore, we have the following side lengths.
• AB = 6 ft
,
• BC = 7 ft
,
• CD = 11 ft
,
• DE = 7 ft
,
• AE = 6 ft
To find the perimeter, let's sum up the side lengths:
Perimeter = AB + BC + CD + DE + AE
Perimeter = 6 + 7 + 11 + 7 + 6
Perimeter = 37 ft
Therefore, the perimeter of the front garage is about 36 ft.
• ANSWER:
A. about 36 ft.