The depreciation equation is given by
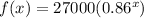
where x represents the number of years. Here, the initial value of the car corresponds to x=0, then we have
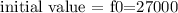
After one year, the car value corresponds to x=1, that is,
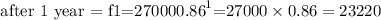
Now, let's find the depreciation percentage by means of a rule of three:
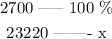
so we have
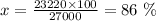
So the difference between 100% and 86% is 14% This means Nichole's car depreciate 14% each year