Question

Distribute 4,350$ among John, Maria, and Betsy, so that Maria receives twice as much as John and Betsy recieves 3 times as much as john

Answer 1

To solve this problem we must generate a system of equations that models its behavior.

To make the problem easier, the money distributed to Jhon, Maria and Betsy will be identified by their initials J, M and B.

`\begin{gathered} M+J+B=4350\to(1) \\ M=2J\to(2) \\ B=3J\to(3) \end{gathered}`

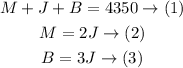
The first thing we are going to do is replace the value of equations (2) and (3) in equation (1)

`\begin{gathered} 2J+J+3J=4350 \\ 6J=4350 \\ J=(4350)/(6) \\ J=725 \end{gathered}`

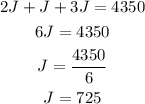
Now we know that John will receive $725 now we plug this value into (2) and (3) to find when Maria and Betsy will receive

`\begin{gathered} M=2J \\ M=2(725) \\ M=1450 \end{gathered}`
`\begin{gathered} B=3J \\ B=3(725) \\ B=2175 \end{gathered}`

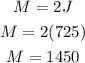
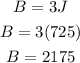
The distribution of the $4350 would be as follows

Maria = $1,450

John = $725

Betsy = $2,175