Given:
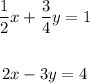
Find-:
The system is dependent, independent, or inconsistent
Explanation-:
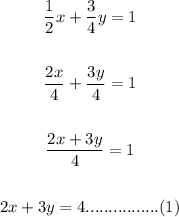

Add both equations then,
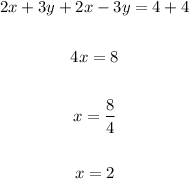
So value of y is:
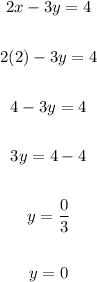
Value of y is 0
The solution for this system of equation is the point (2,0) and this set of equation is consistent since it has one solution at exactly one point. Thus this is consistent and independent.