Question

Hot Air Balloon Tours, Inc. must pay the bank $23,515.27 in interest 200 days after making a loan of $328,120 to purchase hot air balloons. What is the interest rate? Round to the nearest tenth of a percent

Answer 1

To solve this problem we will use the formula for compound interest:

`P_N=P_0\cdot(1+(r)/(k))^N\text{.}`

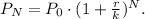
Where:

• P_N is the balance in the account after N years,

,

• P_0 is the starting balance of the account (also called an initial deposit, or principal),

,

• r is the annual interest rate in decimal form,

,

• N in years,

,

• k is the number of compounding periods in one year.

In this problem, we have:

• P_0 = $328,120,,

,

• interest P_N - P_0 = $23,515.27 → ,P_N = $351,635.27,,

,

• N = ,200 days = ,200/365,

,

• k = 1.

From the formula above, we have:

`\begin{gathered} ((P_N)/(P_0))^{(1)/(N)}=1+r \\ r=((P_N)/(P_0))^{(1)/(N)}-1. \end{gathered}`

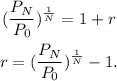
Replacing the data of the problem, we get:

`r=((351,635.27)/(328,120))^{(365)/(200)}-1\cong0.1346\cong13.5％.`

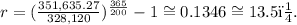
Answer

The annual interest is 13.5%.