parallel
y=2x+11
Step-by-step explanation
Step 1
find the equation of the line:
two lines are parellel if the slope is the same for both,so
let
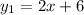
this function is written in slope-intercept form y=mx+b, where m is the slope
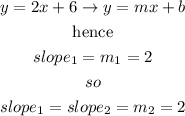
it means the slope of the line we are looking for is 2
Step 2
now,let's find the equation of the line
to do that, we can use this formula:
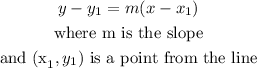
then,let
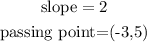
Now,replace in the formula and solve for y
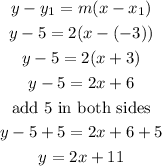
so, the answer is
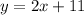
I hope this helps you