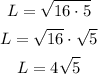The length of the line segment between two points (x1, y1) and (x2, y2) is given by:
![L=\sqrt{\lparen x_2-x_1)^2+\operatorname{\lparen}y_2-y_1)^2}]()
The line segment UV has the endpoints U(3, -5) and (-5, -9). Substituting:
![L=\operatorname{\lparen}-5-3)^2+\operatorname{\lparen}-9+5)^2]()
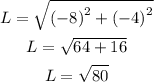
It's required to express the answer in simplified radical form, so we can rewrite the radicand as 80 = 16 * 5: