Answer: Perimeter 88.3 cm
Area 375 sq cm
Step by step explanation:
The perimeter of a triangle is queal to the sum of all the sides. In the figure we have an isosceles triangle (2 sides equal), to find the perimeter we must find the length of the equal sides:
From Pythagorean Theorem we have:
![\begin{gathered} h^2=a^2+b^2 \\ h^2=25^2+15^2 \\ h=\sqrt[]{850}=5\sqrt[]{34} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/soma5aykrf262m37o9uzc6xwmoed2i8c0d.png)
The perimeter is:
![\begin{gathered} P=2\cdot15+5\sqrt[]{34}+5\sqrt[]{34} \\ P=30+5\sqrt[]{34}+5\sqrt[]{34} \\ P=88.309\approx88.3\operatorname{cm} \end{gathered}]()
The area of a triangle can be calculated using the formula:
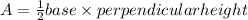
base = 2*15 = 30 cm
Perpendicular height = 25 cm
![\begin{gathered} A=(1)/(2)\cdot30*25 \\ A=375\operatorname{cm} \end{gathered}]()
Perimeter = 88.3 cm
Area = 375 sq cm