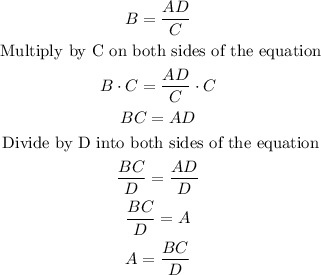To solve the exercise you can take the equations on the right side and solve for A.
So for the first equation on the right side you have:
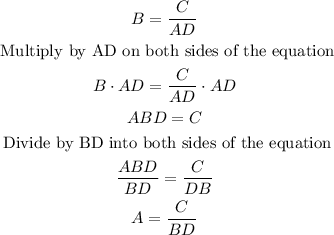
For the second equation on the right side you have:

For the third equation on the right side you have:
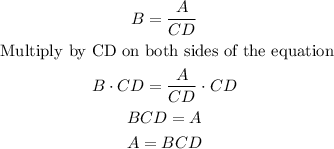
Finally, for the fourth equation on the right side you have: