Question

8 PointsQuestion 15Find the standard form equation of the line that passes through (-1,-4) and (3.-6). For the answer, just enter the coefficient ofthe x-termBlank 1Blank 1Add your answerPointe

Answer 1

The form of the equation that passes through two points is

`y=mx+b`

m is the slope,

b is the y-intercept

The rule of the slope is

`m=(y_2-y_1)/(x_2-x_1)`

Let (x1, y1) = (-1, -4) and (x2, y2) = (3, -6)

`\begin{gathered} m=(-6-(-4))/(3-(-1))=(-6+4)/(3+1) \\ m=(-2)/(4) \\ m=-(1)/(2) \end{gathered}`

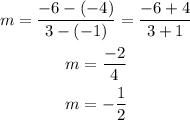
The equation is

`y=-(1)/(2)x+b`

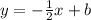
Substitute x by 3 and y by -6 to find b

`\begin{gathered} -6=-(1)/(2)(3)+b \\ -6=-(3)/(2)+b \end{gathered}`

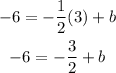
Add 3/2 to both sides

`\begin{gathered} -6+(3)/(2)=-(3)/(2)+(3)/(2)+b \\ -(9)/(2)=b \end{gathered}`

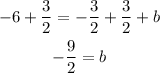
The equation is

`y=-(1)/(2)x-(9)/(2)`

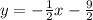
The standard form of the linear equation is

`Ax+By=C`

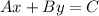
A, B, C are integers

Then multiply all terms in the equation by 2

`2y=-x-9`

Add x to both sides

`\begin{gathered} x+2y=-x+x-9 \\ x+2y=-9 \end{gathered}`

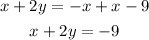
The equation in the standard form is x + 2y = -9