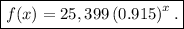Question

Which function models the value of the vehicle in dollars x years after its purchase by

Answer 1

The first option f(x) = 25,399(0.915)^x

Step-by-step explanation:

The price of the vehicle decreases by 8.5% per year. Therefore, after each consecutive year, the price of the vehicle is 100% - 8.5% = 91.5% of the price the previous year.

Now if the price at the beginning is $25,399, then the price after one year will be 91.5% of $25,399.

`price\text{ in the first year}$ =25,399 $*(91.5)/(100)`

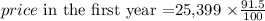
The price after two years then will be

`price\text{ in the second year}=price\text{ in the first year }*(91.5)/(100)`
`\Rightarrow price\text{ in the second year}=25,399*(91.5)/(100)*(91.5)/(100)`

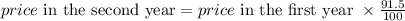
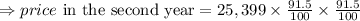
The price after the 3 years then is 91.5% of the price in the second year:

`25,399*(91.5)/(100)*(91.5)/(100)*(91.5)/(100)`

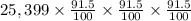
Note that for the first year we multiplied $25,399 by 91.5/100 once, in the second year we multiplied by it twice, and in the third year we multiplied thrice. Therefore, We see a pattern here. The price after x years is $25,399 multiplied by 91.5/100 x times.

In other words, after xth year the price of the vehicle will be

`25,399*((91.5)/(100))^x`

Since 91.5/100 = 0.915, the above becomes

`25,399(0.915)^x`

If we represent this price by f(x) then we have

`\boxed{f\mleft(x\mright)=25,399\left(0.915\right)^x.}`