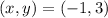Question

X+y=2 y=2x+5write the solution as an ordered pair

Answer 1

We are given the following system of equations:

`\begin{gathered} x+y=2,(1) \\ y=2x+5,(2) \end{gathered}`

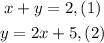
To solve this system we will use the method of substitution. We will replace the value of "y" from equation (2) into equation (1).

`x+2x+5=2`

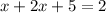
Now we will add like terms:

`3x+5=2`

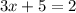
Now we will subtract 5 to both sides of the equation:

`\begin{gathered} 3x+5-5=2-5 \\ 3x=-3 \end{gathered}`

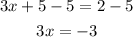
Now we will divide by 3:

`x=-(3)/(3)=-1`

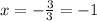
Now we will replace the value of "x" in equation (2):

`y=2(-1)+5`

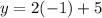
Solving the operations:

`\begin{gathered} y=-2+5 \\ y=3 \end{gathered}`

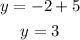
The solution of the system is:

`(x,y)=(-1,3)`