Question

The area of a rectangle can be represented by the expression 4x^2+8x+9 If the area of the rectangle is 69 square inches, what is the value of x, the width of the rectangle, in inches?

Answer 1

Step-by-step explanation

`A=4x^2+8x+9`

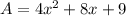
Step 1

Let

A=96 (square inches)

so,replacing

`\begin{gathered} A=4x^2+8x+9 \\ 69=4x^2+8x+9 \\ \text{now, to set the equation equal to zero subtract 69 in both sides} \\ 69-69=4x^2+8x+9-69 \\ 0=4x^2+8x-60\Rightarrow equation\text{ (1)} \end{gathered}`

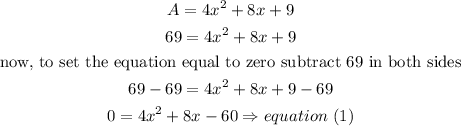
Step 2

now, we need to solve the quadratic equation,we can use the quadratic formula

`\begin{gathered} 4x^2+8x-60=0\Rightarrow ax^2+bx+c \\ thus \\ a=4 \\ b=8 \\ c=-60 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{replace} \\ x=\frac{-8\pm\sqrt[]{8^2-4(4)(-60)}}{2(4)} \\ x=\frac{-8\pm\sqrt[]{1021}}{8} \\ x=(-8\pm32)/(8) \end{gathered}`

therefore, the solutions are

`\begin{gathered} x=(-8\pm32)/(8) \\ x_1=(-8+32)/(8)=(24)/(8)=3 \\ x_2=(-8-32)/(8)=(-40)/(8)=-5 \end{gathered}`

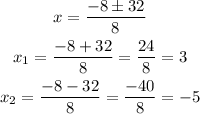
as we are looking for a distance, the ONLY valid answer must be positive

so, the answer is

x=3

I hope this helps you

x