Question

Can u help pls n make it neat bc :))

Answer 1

(a)26.1 bulb per month on average

(b)6.5

Step-by-step explanation:

The number of burnt bulbs recorded over 10 months is given below:

`23,25,21$,$33,17,39,26,24,31,22`

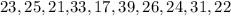
Part A

To find the average, add up all the numbers and divide by 10.

`\begin{gathered} \text{Average}=(23+25+21$+$33+17+39+26+24+31+22)/(10) \\ =(261)/(10) \\ =26.1 \end{gathered}`

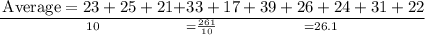
The average number of bulbs that burn out each month is 26.1.

Part B

To find the standard deviation, we use the formula below:

`\begin{gathered} \text{Standard Deviation}=\sqrt[]{\frac{\sum (x-\bar{x})^2}{n-1}} \\ \bar{X}=26.1 \end{gathered}`

The data is presented in the table below:

From the table above:

`\sum (x-\bar{x})^2=378.9`

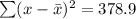
Therefore:

`\begin{gathered} \text{Standard Deviation}=\sqrt[]{\frac{\sum (x-\bar{x})^2}{n-1}}=\sqrt[]{(378.9)/(10-1)} \\ =\sqrt[]{(378.9)/(9)} \\ =\sqrt[]{42.1} \\ =6.5\text{ (to 1 decimal place)} \end{gathered}`

The standard deviation is 6.5.