Question

he vertices of ABC represent theuoy markers that form the legs ofne course for a swim race. What is theHistance from marker C to marker A?Round your answer to the nearest tenthof a meter.А65°200 m35°116.5 m148.4 m175.9 m269.5 m

Answer 1

We are given the following information

From this picture, we want to find the vaule of x. To so, we will use the sine law. to solve this problem.

The sine law relates the sine of the angles of the triangle and the length of the opposite sides of the triangle. If we have a triangle of the form

Then,the sine law states that

`(\sin(A))/(a)=(\sin(C))/(c)=(\sin (B))/(b)`

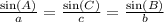
Which is equivalent to

`(a)/(\sin(A))=(c)/(\sin(C))=(b)/(\sin (B))`

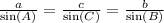
In our case, we are given the measure of angles A and B and missing the measure of angle C. Also, we are given the measure of side c. If we apply the sine law to the given triangle we have

`(x)/(\sin(35))=(200)/(\sin (C))`

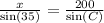
So, first we need to identify the value of C. To do so, we will use the following fact

The sum of the inner angles of a triangle is 180°.

Then, we have the following equation

`65+35+C=180`

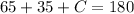
If we operate on the left side, we get

`100+C=180`

So, by subtracting 100 from both sides, we get

`C=180-100=80`

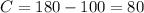
So, if we replace the value of C in the equation we had, we get

`(x)/(\sin(35))=(200)/(\sin (80))`

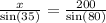
If we multiply both sides by sin(35) we get

`x=(200\cdot\sin (35))/(\sin (80))`

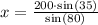
so, using a calculator we get

`x=(200\cdot\sin (35))/(\sin (80))\approx116.48495548\approx116.5`

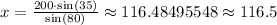
so the value of x is approximately 116.5 meters