1. it is not an arithmetic sequence
2.arithmetic sequence
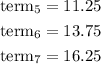
Step-by-step explanation
Step 1
find the common difference for the sequence.
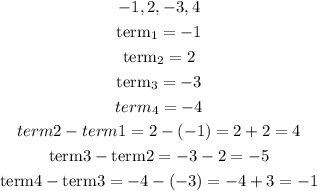
there is no common difference , so this is not an arithmetic sequence
Step 2
2.
find the common difference

so, the common difference is 2.5, in other words, it means you have to add 2.5 to obtain the next term
Step 2.1
now, let's find the next three terms

I hope this helps you