Question

Enter the values of X & Y in the solution for each system in the following table

Answer 1

System 1

`\begin{gathered} 3x\text{ - 4y = 6} \\ x\text{ + 4y = 18} \end{gathered}`

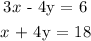
Using Elimination method:

Add equation 1 to equation 2:

`\begin{gathered} (3x\text{ -4y\rparen +}(x\text{ + 4y\rparen = 6 + 18} \\ 3x\text{ - 4y + x + 4y = 24} \\ Collect\text{ like terms} \\ 3x\text{ + x -4y + 4y = 24} \\ 4x\text{ = 24} \\ x\text{ = }(24)/(4) \\ x\text{ = 6} \end{gathered}`

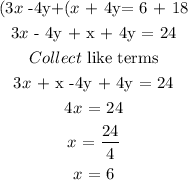
Substitute the value of x into any of the equation and solve for y

`\begin{gathered} x\text{ + 4y = 18} \\ 6\text{ + 4y = 18} \\ Collect\text{ like terms} \\ 4y\text{ = 18-6} \\ 4y\text{ = 12} \\ y\text{ = }(12)/(4) \\ y\text{ =3} \end{gathered}`

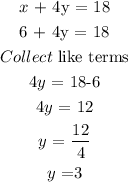
Solution: (6,3)

System 2:

`\begin{gathered} 3x\text{ - 4y = -3} \\ 4x\text{ - 3y = 10} \end{gathered}`

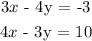
Using Elimination method

Multiply the first equation by 3 and the second by 4

`\begin{gathered} 9x\text{ - 12y = -9} \\ 16x\text{ - 12y =40} \end{gathered}`

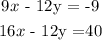
Subtract the resulting first equation from the second:

`\begin{gathered} (16x\text{ - 12y\rparen - \lparen9x - 12y\rparen = 40 -\lparen-9\rparen} \\ 16x\text{ - 12y - 9x + 12y =49} \\ Collect\text{ like terms} \\ 16x\text{ -9x - 12y + 12y = 49} \\ 7x\text{ = 49} \\ Divide\text{ both sides by 7} \\ (7x)/(7)\text{ = }(49)/(7) \\ x\text{ = 7} \end{gathered}`

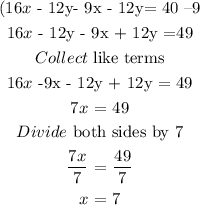
Substitute the value of x into any of the equation and solve for y

`\begin{gathered} 4x\text{ -3y =10} \\ 4*7\text{ - 3y =10} \\ 28\text{ - 3y = 10} \\ Collect\text{ like terms} \\ -3y\text{ = 10-28} \\ -3y\text{ = -18} \\ y\text{ = }(-18)/(-3) \\ y\text{ =6} \end{gathered}`

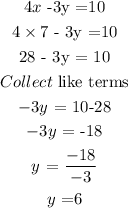
Solution: (7,6)

Answer Summary