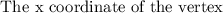Question

The answers in blank boxes are either 1. The x intercept 2.The P intercept 3. The X coordinate of the the vertex4. The P coordinate of the vertex

Answer 1

a) The startup cost of the company is the value of P when x equals zero.

Which is the P intercept on the graph.

`\text{The P intercept}`

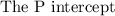
b) The number of items they have to sell to break even is the value of x when the profit P equals zero.

This is the x-intercept on the graph.

`\text{The x intercept}`

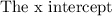
c) The number of products they need to sell to maximize profit is the value of x at the maximum point on the graph.

This is the x coordinate of the vertex

`\text{ The x coordinate of the vertex}`

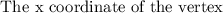
Step-by-step explanation:

Given the revenue equation of the product;

`P(x)=-2x^2+950x-14000`

Graphing the equation.

a) The startup cost of the company is the value of P when x equals zero.

Which is the P intercept on the graph.

`\text{The P intercept}`

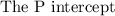
b) The number of items they have to sell to break even is the value of x when the profit P equals zero.

This is the x-intercept on the graph.

`\text{The x intercept}`

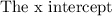
c) The number of products they need to sell to maximize profit is the value of x at the maximum point on the graph.

This is the x coordinate of the vertex

`\text{ The x coordinate of the vertex}`