Question

Find the equation of the line through the given points (-1, 0) and (5, 5)

Answer 1

Answer:

5x - 6y = -5

Explanations:

The equation of the line passing through the points (x₁, y₁) and (x₂, y₂) is given as:

y - y₁ = m (x - x₁)

where m is the slope of the line and is given by the formula:

m = (y₂ - y₁) / (x₂ - x₁)

For the line passing through the points (-1, 0) and (5, 5)

`\begin{gathered} x_1=-1,y_1=0,x_2=5,y_2=5 \\ m\text{ = }(y_2-y_1)/(x_2-x_1) \\ m\text{ = }(5-0)/(5-(-1)) \\ m\text{ = }(5)/(6) \end{gathered}`

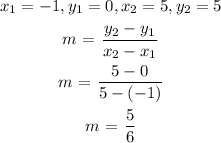
Substitute the values of x₁, y₁, and m into the equation of the line:

y - y₁ = m (x - x₁)

`\begin{gathered} y\text{ - 0 = }(5)/(6)(x\text{ - (-1))} \\ y\text{ = }(5)/(6)\text{ (x + 1)} \\ y\text{ = }(5)/(6)x\text{ + }(5)/(6) \end{gathered}`

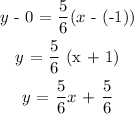
6y = 5x + 5

5x - 6y = -5

The equation of the line is:

5x - 6y = -5