Given data:
* The force acting on the suitcase is 25 N.
* The work done on the suitcase is,
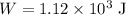
* The suitcase moved the distance is 51 m.
Solution:
The workdone in terms of force and displacement is,
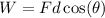
where F is the force, d is the displacement,
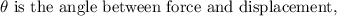
Substituting the known values,
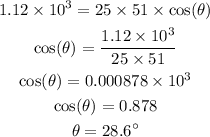
Thus, the angle above the horizontal at which the force is oriented is 28.6 degree.