We are given that a ball is dropped down a ramp and we are asked to determine the velocity and construct a velocity table.
To do that we need to use the following formula for velocity:
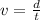
Where:
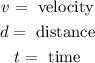
For example, for the case when the ball is stopped after 2 meters we determine the velocity by dividing the distance over the time, we get:
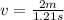
Solving the operations we get:

Therefore, the velocity for this distance is 1.7 meters per second.
We repeat this operation for each of the distances with the corresponding time and construct a table of "time" vs "velocity", as follows:
To build the graph we plot the points of time and velocity, as follows: