The series is given to be:
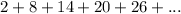
The nth term is given to be 1704.
The formula to calculate the nth term is given to be:
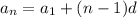
where a₁ is the first term and d is the common difference.
The sum of the sequence can be calculated using the formula:
![S_n=(n)/(2)[2a+(n-1)d]](https://img.qammunity.org/2023/formulas/mathematics/college/hnepadwec5k1zyh7z2da1zhp4bypusawoc.png)
From the series, we have:
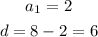
Therefore, the sum of the nth term can be calculated as shown below:
![\begin{gathered} 1704=(n)/(2)[2\cdot2+(n-1)6] \\ \mathrm{Multiply\:both\:sides\:by\:}2 \\ 1704\cdot \:2=(n)/(2)\left[2\cdot \:2+\left(n-1\right)\cdot \:6\right]\cdot \:2 \\ 3408=n\left(4+6\left(n-1\right)\right) \\ Expanding\text{ }parentheses \\ 3408=6n^2-2n \\ \mathrm{Subtract\:}3408\mathrm{\:from\:both\:sides} \\ 6n^2-2n-3408=3408-3408 \\ 6n^2-2n-3408=0 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/vmpogjh6igw6b424ytdnr2o7jzg3t5nhql.png)
Using the quadratic formula to solve, we have:
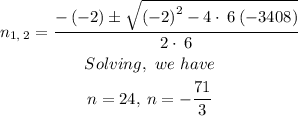
Since the number cannot be negative or a decimal/fraction, the term number will be 24.