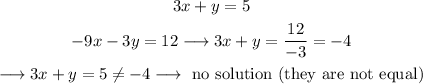The slope intercept form of a line is:

Then we can write each of the equations as:
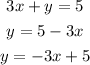
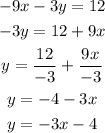
We have parallel lines, as they both have the same slope (m=-3).
If we graph the lines, we get:
The lines don't intersect, so we have no solution.
We can demonstrate this as: