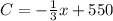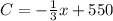
1) We can begin by writing C as a function of x and find the slope between two points (300,450) and (150,500)
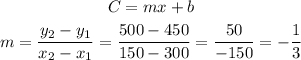
2) Now that we know the slope, we need to find the linear coefficient (y-intercept), using one of those ordered pairs: (150,500)
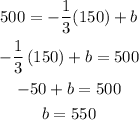
So the function is: