Question

A block attached to a horizontal spring with a spring constant k = 200 N/m is displaced to x = +6 cm and released from rest. The time needed for the block to reach x = +6 cm for the first time is 0.2 sec. Determine the maximum restoring force applied on the block and its maximum acceleration.

Answer 1

Given:

The spring constant of the spring is k = 200 N/m

The maximum displacement of the spring is x = 6 cm = 0.06 m

The time period is T = 0.2 s

To find the maximum restoring force and the maximum acceleration.

Step-by-step explanation:

The maximum restoring force applied on the block can be calculated as

`\begin{gathered} F=kx \\ =200*0.06\text{ } \\ =\text{ 12 N} \end{gathered}`

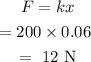
First, we need to calculate angular frequency.

The angular frequency can be calculated as

`\begin{gathered} \omega=(2\pi)/(T) \\ =(2*3.14)/(0.2) \\ =31.4\text{ rad/s} \end{gathered}`

The maximum acceleration can be calculated as

`\begin{gathered} a=x\omega^2 \\ =0.06*(31.4)^2 \\ =59.2m/s^2 \end{gathered}`

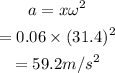
Final Answer: The maximum restoring force is 12 N and the maximum acceleration is 59.2 m/s^2.