Question

R(-9,4) and S(2,-1) Find T ..... Where S is the Midpoint of RTS(-4,-6) and T(-7,-3) Find R ..... Where S is the midpoint of SR

Answer 1

The coordinate of the point T is (13, -6)

The coordinate of the point R is (-1, 9)

Step-by-step explanation:

Given the points R(-9,4) and S(2, -1), where S is the midpoint of RT, we want to find T.

The coordinate of the midpoint of a line is given by the formula:

`M=((x_1+x_2)/(2),(y_1+y_2)/(2))`

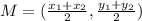
Since S is the midpoint, then

`((x_1+x_2)/(2),(y_1+y_2)/(2))=(2,-1)`

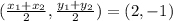
Where:

`\begin{gathered} x_1=-9 \\ y_1=4 \\ x_2=? \\ y_2=\text{?} \end{gathered}`

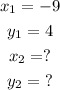
So,

`\begin{gathered} (x_1+x_2)/(2)=2 \\ \\ (y_1+y_2)/(2)=-1 \end{gathered}`

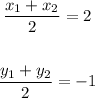
Implies:

`\begin{gathered} \frac{-9_{}+x_2}{2}=2 \\ \\ -9+x_2=4 \\ x_2=4+9=13 \end{gathered}`
`\begin{gathered} \frac{4_{}+y_2}{2}=-1 \\ \\ 4+y_2=-2 \\ y_2=-2-4=-6 \end{gathered}`

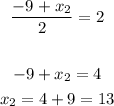
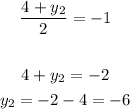
Therefore, T = (13, -6)

........................................................................................................................

Given S(-4, -6) and T(-7, -3)

Following the same steps as the one above, we want to find R, where T is the midpoint.

Here, the given parameters are:

`\begin{gathered} x_2=-7 \\ y_2=-3 \end{gathered}`
`\begin{gathered} x_1,y_1 \\ \text{are the unknown } \end{gathered}`

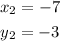
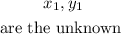
Now, we have:

`\begin{gathered} (x_1+x_2)/(2)=-7 \\ \\ (y_1+y_2)/(2)=-3 \end{gathered}`
`\begin{gathered} (x_1-7)/(2)=-4 \\ \\ x_1-7_{}=-8 \\ \\ x_1=-8+7=-1 \end{gathered}`
`\begin{gathered} (y_1-3)/(2)=-6 \\ \\ y_1-3=-12 \\ \\ y_1=-12+3=-9 \end{gathered}`

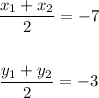
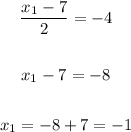
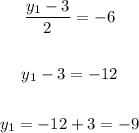
The coordinate of the point R is (-1, 9)